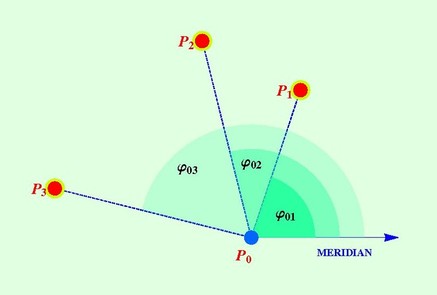
Jan Vermeer (1632 - 1675) Der Geograph

Die Snellius-Pothenotsche Aufgabe

Aus drei der Lage nach bekannten Punkten A,B,C den eigenen Standort D bestimmen. Holzschnitt in einem Buch von Adolph Poppe 1847

Snellius-Pothenot Problem: Bestimmung der Koordinaten des Punktes P0 aus drei der Lage nach bekannten Punkten P1, P2 und P3 und ihren zu einem beliebigen Meridian gemessenen Azimuthen. Die schönste Lösung gelingt in einer Geometrie mit komplexen Zahlen.

Schon im Gymnasium hat mich eine mathematische Aufgabe fasziniert, die auf den ersten Blick unlösbar schien. Es ging um das Rückwärtseinschneiden nach drei der Lage nach bekannten Punkten in einer Ebene. In der Schule löste man damals die Aufgabe durch komplizierte trigonometrische Formeln - das Ganze ziemlich unelegant.

Die Situation änderte sich schlagartig, als ich als Student in der Bibliothek des Astronomischen Institutes und im Mathematischen Institut der Universität Münster die Werke von C.F. Gauß entdeckte. Im Band 8 der gesammelten Werke standen Notizen von Gauss über dieses Problem, die ein Zeitintervall von etwa 1810 bis etwa 1845 umspannten. Gauß rechnete mit komplexen Koordinaten und seine Formeln waren das non plus ultra an Eleganz. Endlich hatte ich die Formeln gefunden, die dem Problem wirklich angemessen sind. Merkwürdigerweise habe ich aber nie eine direkte baryzentrische Endformel für den gesuchten Neu-Punkt bei Gauß gefunden. Der berühmte niederländische Geodät J.M. Tienstra (1895-1951) hat um 1935 seine bekannte baryzentrische Formel für den Neupunkt aufgestellt, die meiner komplexen baryzentrischen Formel sehr ähnlich ist. Ich bin in den folgenden Jahren immer wieder auf die algebraische Struktur der Formeln und ihrer geometrischen Deutung zurückgekommen, bis ich sie weitgehend verstanden habe. Insbesondere das alte physische Kriterium für die Verträglichkeit der Beobachtungsdaten nach Gauß hat mir einiges Kopfzerbrechen bereitet. Gottfried Wagener (1831-1892), der später als Ingenieur in Japan zu Ruhm gelangt ist, hat noch in Göttingen 1852 eine kleine Dissertation zu diesem Problem geschrieben, nachdem er in einer Vorlesung bei Gauss von diesem Problem gehört hatte.

Wenn ich es richtig gelesen habe, gibt es heute über 100 unterschiedliche geometrische und analytische Lösungsmethoden für das Problem. Ein wirklich bemerkenswertes Problem....

Das Problem kann auf das sogenannte Achtpunktproblem erweitert werden, bei dem auf der einen Seite drei oder vier Beobachtungsstationen und in der Ferne fünf oder vier Landmarken sichtbar sind. Nur durch Winkelmessungen zwischen den Landmarken kann man dann alle acht Punkte in ihrer relativen Lage festlegen, wenn man die Koordinaten zweier Landmarken willkürlich vorgibt. Lambert und Clausen haben dieses schwierige Problem 1765 und 1842 gelöst.

Die Pothenotsche Aufgabe
eBook
snellius_pothenot.pdf
PDF-Dokument [3.2 MB]

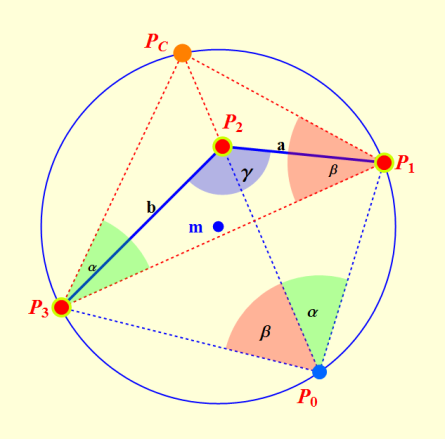
Konstruktion der Pothenotschen Aufgabe nach Collins (1671)

Durch Antragen der Winkel beta bei P1 und alpha bei P3 an den gemeinsamen Schenkel P1P3 schneiden sich die freien Schenkel im Collinspunkt PC. Die drei Punkte P1 - P3 - PC definieren einen Kreis, auf dem auch der gesuchte Punkt P0 liegt. Dieser ergibt sich als Schnittpunkt der verlängerten Geraden PC-P2 mit diesem Umkreis.

Aktuelles

kritisch betrachtet

Eine neue Computersimulation im Jahre 2023 des Kosmos (Flamingo project) hat nicht nur Dunkle Materie, sondern auch baryonische Materie und galaktische Winde berücksichtigt. Die Hoffnungen, die S8-Anomalie der Strukturbildung dadurch zu klären, wurden aber enttäuscht. Ursache: anstatt w=-1 (Kosmologische Konstante) doch w = -2/3?

Eine kleine historische Sensation hat sich Ende 2022 in Belgien ereignet: Das verloren geglaubte einzige Videointerview mit George Lemaitre (1894-1966) aus dem Jahre 1964 wurde in einem Archiv wiedergefunden. Es war falsch eingeordnet worden. Nicht nur auf youtube kann man es finden, sondern es existiert inzwischen (Januar 2023) auch eine schriftliche Transkription [arXiv:2301.07198v2] in französischer und englischer Sprache. Ich beabsichtige, dieses legendäre Interview zeitnah ins Deutsche zu übersetzen.

Ende 2018 entstand weltweit ein riesiger Medienrummel (Medien-Hype), leider auch unterstützt von der Oxford University, dass das Problem der dunklen Materie und der Dunklen Energie durch die Einführung von zusätzlichen negativen Massen (dark fluid) mit zusätzlicher kontinuierlicher Materie-Erzeugung im Universum sehr einfach gelöst werden könne. Ursache sei einfach ein Vorzeichenfehler, behauptete Jamie Farnes von der Oxford University. (A&A 620, id. A92, 2018) Sofort tauchten aber Gegenstimmen auf, welche die Unmöglichkeit von negativen Massen (träger Masse,schwerer Masse, gravitativer Masse) im Rahmen der Einsteinschen Theorie darlegten. Zudem zeigte sich im Laufe des Jahres 2019 ein schwerer Fehler im Simulations-Programm und die Tatsache, dass sich im Rahmen dieser gewagten These und ihrer korrigierten Simulation die Halos um Galaxien nicht in der beobachten postulierten Form (dunkle Materie) bilden können. Ein öffentlicher Widerruf dieser fehlerhaft falschen Hypothese hat aber nie stattgefunden! Historisch kann man diese Affäre als den NEGATIVE MASS BUG bezeichnen.

Hinweise auf eine angebliche Phase der "Inflation" im frühen Universum zerfallen zu Staub: Im März 2014 veranstaltete ein Team um den Harvard Astronomen J. Kovac (BICEP2) für eine völlig übereilte propagandistische Pressekonferenz (schon einen Tag vorher als Sensation angekündigt!): Man hat in der Hintergrundstrahlung des Universums Signaturen einer Polarisation entdeckt, die angeblich eindeutig auf Gravitations-wellen in einer Inflationsphase des frühen Universums schließen lassen. Der eigentliche Skandal ist, daß man die Daten fast ausschließlich durch MIE-Streuung von Mikrowellen an inter-stellaren Staubteilchen erklären kann und muss - und genau daran hatte das "Team" bei der Auswertung nur sehr unzulänglich gedacht! Ein aggessiver Versuch, die Öffentlichkeit durch Sensation zu täuschen und eine nicht überprüfbare (nicht falsi-fisierbare) Theorie (Inflations - Hypothese) salonfähig zu machen. Der Citation-Index dieser Veröffentlichung ist inzwischen wesentlich höher als ihr Widerruf. Die Raffgier nach Forschungs-geldern und Nobelpreisen treibt auch in der Wissenschafts - Industrie immer bizarrere Blüten...

Nachweis angeblich überall im Universum vorhandener DUNKLER MATERIE in Form von Elementarteilchen gescheitert! Das bis jetzt empfind-lichste Experiment LUX in Sanford/South Dakota USA konnte in einer ersten Phase Ende Oktober 2013 keine WIMPs - Teilchen feststellen, die angeblich einen großen Teil der angeblich existierenden Dunklen Materie ausmachen sollen. Alle früheren angeblichen Nachweise sind somit fehlerhaft gewesen. Ein sehr wichtiges, schönes und befriedigendes Resultat! "Die Sekte der Gläubigen an die "Dunkle Materie", die sich selber als alternativlos ansieht, bleibt so weiter in der Krise. Die Hypothese der "Dunklen Materie" ist allerdings im Sinne von Ockhams Rasiermesser die wahrscheinlichste "Minimalhypothese", da sie extrem einfach ist und jede dynamische Anomalie durch Hinzufügen exotischer Materie erklären kann. Ob allerdings so in der Zukunft der von Teilchenphysikern geschürte "Big Science" Teilchen-Lobbyismus mit der platten Devise - Wir verstehen nichts, können aber alles erklären - das vorherrschende Dogma bleiben wird, wissen nur die Sterne...