Die Zarenkanone (Zar - puschka) von 1586 am Moskauer Kreml
(wikimedia commons)
Die ballistische Kurve
Wenn man in der Geschichte der Differentialrechnung des 18. Jahrhunderts blättert, begegnen einem viele interessante Probleme, für die damalige Akademien Preisaufgaben gestellt haben. Und im Laufe der Gymnasialzeit lernte man einige seltsame Kurven der höheren Mathematik kennen - z.B. die Kettenlinie (Theorie der Hängebrücken) oder die Brachistochrone. Doch eine Kurve blieb ein völliges Mysterium: die ballistische Kurve. Man findet hier in der heutigen Literatur keine analytische Formel mehr - außer natürlich die klassische Wurfparabel.
Dabei hat die Theorie der Bahnkurve eine aufregende Geschichte - selbst ein I. NEWTON ist an diesem Problem gestrauchelt. J. BERNOULLI hat als Erster 1719 eine analytische Lösung gegeben, nachdem er I. NEWTON einen Fehler in der ersten Ausgabe der Principia Mathematica nachgewiesen hatte. 1745 gab dann L. EULER eine längere Abhandlung mit Reihenentwicklungen, die aber für die Auswertung unbrauchbar waren. Zu einem gewissen Abschluß gelangten die Untersuchungen durch eine umfangreiche Arbeit von J.H. LAMBERT 1766. Hier steht auch eine einfache genäherte analytische Formel für die ballistische Kurve - die aber heute keiner mehr kennt. Ein Grund dafür könnte sein, dass der Preußenkönig Friedrich II. 1781 das Buch von G.F.TEMPELHOFF "Le Bombadier Prussien" und alle damit zusammenhängenden Fragen unter militärische Geheimhaltung stellte...
Da ich dieses Kurvenproblem für sehr interessant halte und es offensichtlich wesentlich schwieriger als das gravitative Zweikörperproblem nach NEWTON ist, folgt hier mein kleines eBook zu diesem Thema.
Ballistische Kurven mit einem Wendepunkt
Ein besonderes ballistisches Problem stellt der Wiedereintritt einer Raumkapsel in eine Planetenatmosphäre dar. Hier müssen besondere Bedingungen an den Eintrittswinkel gestellt werden, damit einerseits der Winkel nicht zu flach ist und der Körper auf seiner Parabelbahn ins All zurückkehrt, andererseits aber auch nicht zu steil, damit die Bremsbeschleunigung für einen Menschen im erträglichen Rahmen bleibt und die thermische Erhitzung des "Blunt Body" den kritischen Grenzwert nicht überschreitet (J.H. Allen, A. Eggers, 1958). Relativ zur Planetenoberfläche kann die ballistische Kurve dabei S-förmig (liegendes "S") sein, obwohl - im Gegensatz zu den Apollokapseln - praktisch kein Auftrieb wirkt. Beim rein ballistischen Wiedereintritt aus einer Kreisbahn ohne Auftrieb ergibt die vom russischen Aerodynamiker V.A. Yaroshevsky (1932-2014) abgeleitete Differentialgleichung die maximale Bremsbeschleunigung zu c*g*sqrt[R/H], wobei g die Erdbeschleunigung, R den Erdradius und H die Skalenhöhe der Atmosphäre bezeichnen. Für die Konstante c gilt 0.27566..., ein Wert, der in der Literatur mit leicht unterschiedlichen Werten ab der dritten Nachkommastelle angegeben wird.
Das Eindringen eines Riesenboliden in die Erdatmosphäre erinnert an das Tunguska-Phänomen in Sibirien von 1908 und motiviert dazu, sich mit der "Blast Wave" Theorie (point source solution) zu beschäftigen. Welche Schockgeschwindigkeiten entstehen bei welcher Energie in welcher Entfernung?
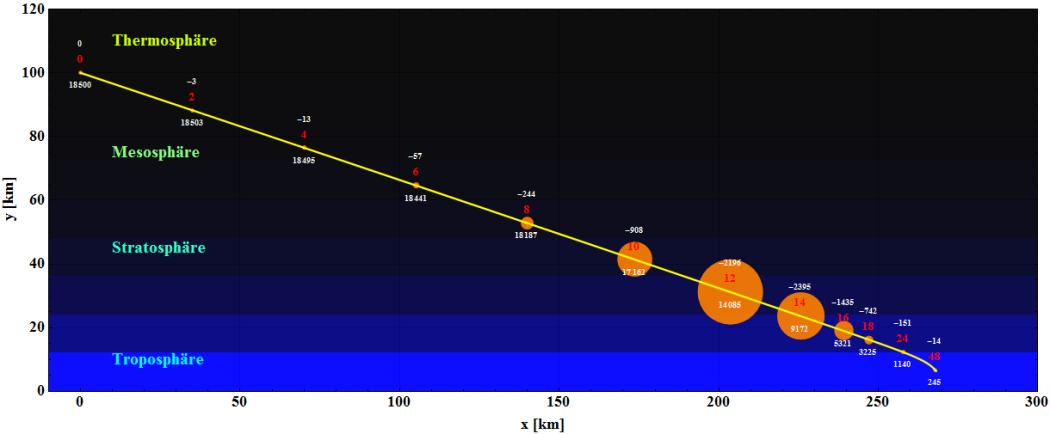
Hypersonischer Raumgleiter
Beispiel einer semi-ballistischen Bahnkurve bei einem hypersonischen Gleitkörper, welcher in der oberen Atmosphäre aufgrund des starken Dichtegradienten mit der Höhe und seines Auftriebbeiwertes rikoschettartige Wellenbewegungen durchführt. Die Wellenlänge wird durch den Auftriebsbeiwert und die Skalenhöhe der mit der Höhe exponentiell abfallenden Atmosphärendichte bestimmt. Es handelt sich also im strengen Sinne nicht um die klassische Phygoide (Längsschwingungen) bei Luftfahrzeugen in niedrigen Höhen. Die beste Analogie wäre ein Stein, der sehr flach über die Wasseroberfläche geworfen wird und dabei immer kleiner werdende Sprünge macht, bis er im Wasser versinkt. Die weißen Zahlen bedeuten die Zeit in Sekunden, die roten Zahlen Geschwindigkeiten in m/s. Erste ausführliche Rechnungen zu solchen Bahnen hat der Raumfahrtingenieur E. Sänger (1905-1964) mit seiner Assistentin I. Bredt (1911-1984) im Jahre 1941 durchgeführt (Geheimprojekt "Silbervogel" 1944). Aufgrund der immensen thermischen Belastung ist die technische Ausführung allerdings auch heute noch extrem schwierig (Space Shuttle).
Aktuelles
kritisch betrachtet
Eine neue Computersimulation im Jahre 2023 des Kosmos (Flamingo project) hat nicht nur Dunkle Materie, sondern auch baryonische Materie und galaktische Winde berücksichtigt. Die Hoffnungen, die S8-Anomalie der Strukturbildung dadurch zu klären, wurden aber enttäuscht. Ursache: anstatt w=-1 (Kosmologische Konstante) doch w = -2/3?
Eine kleine historische Sensation hat sich Ende 2022 in Belgien ereignet: Das verloren geglaubte einzige Videointerview mit George Lemaitre (1894-1966) aus dem Jahre 1964 wurde in einem Archiv wiedergefunden. Es war falsch eingeordnet worden. Nicht nur auf youtube kann man es finden, sondern es existiert inzwischen (Januar 2023) auch eine schriftliche Transkription [arXiv:2301.07198v2] in französischer und englischer Sprache. Ich beabsichtige, dieses legendäre Interview zeitnah ins Deutsche zu übersetzen. Bis jetzt kannte man nur ein schriflich niedergelegtes Interview aus dem Jahre 1938.
Ende 2018 entstand weltweit ein riesiger Medienrummel (Medien-Hype), leider auch unterstützt von der Oxford University, dass das Problem der dunklen Materie und der Dunklen Energie durch die Einführung von zusätzlichen negativen Massen (dark fluid) mit zusätzlicher kontinuierlicher Materie-Erzeugung im Universum sehr einfach gelöst werden könne. Ursache sei einfach ein Vorzeichenfehler, behauptete Jamie Farnes von der Oxford University. (A&A 620, id. A92, 2018) Sofort tauchten aber Gegenstimmen auf, welche die Unmöglichkeit von negativen Massen (träger Masse,schwerer Masse, gravitativer Masse) im Rahmen der Einsteinschen Theorie darlegten. Zudem zeigte sich im Laufe des Jahres 2019 ein schwerer Fehler im Simulations-Programm und die Tatsache, dass sich im Rahmen dieser gewagten These und ihrer korrigierten Simulation die Halos um Galaxien nicht in der beobachten postulierten Form (dunkle Materie) bilden können. Ein öffentlicher Widerruf dieser fehlerhaft falschen Hypothese hat aber nie stattgefunden! Historisch kann man diese Affäre als den NEGATIVE MASS BUG bezeichnen.
Hinweise auf eine angebliche Phase der "Inflation" im frühen Universum zerfallen zu Staub: Im März 2014 veranstaltete ein Team um den Harvard Astronomen J. Kovac (BICEP2) für eine völlig übereilte propagandistische Pressekonferenz (schon einen Tag vorher als Sensation angekündigt!): Man hat in der Hintergrundstrahlung des Universums Signaturen einer Polarisation entdeckt, die angeblich eindeutig auf Gravitations-wellen in einer Inflationsphase des frühen Universums schließen lassen. Der eigentliche Skandal ist, daß man die Daten fast ausschließlich durch MIE-Streuung von Mikrowellen an inter-stellaren Staubteilchen erklären kann und muss - und genau daran hatte das "Team" bei der Auswertung nur sehr unzulänglich gedacht! Ein aggessiver Versuch, die Öffentlichkeit durch Sensation zu täuschen und eine nicht überprüfbare (nicht falsi-fisierbare) Theorie (Inflations - Hypothese) salonfähig zu machen. Der Citation-Index dieser Veröffentlichung ist inzwischen wesentlich höher als ihr Widerruf. Die Raffgier nach Forschungs-geldern und Nobelpreisen treibt auch in der Wissenschafts - Industrie immer bizarrere Blüten...
Nachweis angeblich überall im Universum vorhandener DUNKLER MATERIE in Form von Elementarteilchen gescheitert! Das bis jetzt empfind-lichste Experiment LUX in Sanford/South Dakota USA konnte in einer ersten Phase Ende Oktober 2013 keine WIMPs - Teilchen feststellen, die angeblich einen großen Teil der angeblich existierenden Dunklen Materie ausmachen sollen. Alle früheren angeblichen Nachweise sind somit fehlerhaft gewesen. Ein sehr wichtiges, schönes und befriedigendes Resultat! Die Hypothese der "Dunklen Materie" ist allerdings im Sinne von Ockhams Rasiermesser die wahrscheinlichste "Minimalhypothese", da sie extrem einfach ist und jede dynamische Anomalie durch Hinzufügen exotischer Materie erklären kann. Im Rahmen der Gravitationstheorie (nicht Elementarteilchen - Theorie) wären aber dann "black holes" unterschiedlicher Massen die wahrscheinlichsten Objekte für Dunkelmaterie (Schon Laplace hatte dies 1799 vermutet) Sie wären so etwas wie "die ungeborenen Sterne" des Kosmos, da bei Ihnen die Gasakkretion nicht stattfand oder nicht stattfinden kann. Ob allerdings in der Zukunft der von Teilchenphysikern geschürte "Big Science" Teilchen-Lobbyismus mit der platten Devise - Wir verstehen nichts, können aber alles erklären - das vorherrschende Dogma bleiben wird, wissen nur die Sterne...