Verschiedenartiges und Gemischtes
Geometrie und Sangaku
Seit meiner Schulzeit übten Probleme der Geometrie eine magische Faszination aus, der ich mich nicht entziehen konnte. Häufig interessierten mich hier aber nicht Beweise im "griechischen Geiste", sondern mehr elegante Lösungen im Rahmen der analytischen Methode. Man kann in der Vergangenheit viele Anregungen bekommen, die hier in zwangloser Folge gesammelt werden sollen. Dazu gehört zum Beispiel das große Feuerbach - Theorem, das Pascal Theorem und andere vergessenen Sätze der Geometrie.
Aber auch die Theorie des Kugelpendels und des Foucaultpendels in projektiven Koordinaten wird man in der heutigen Literatur schwerlich finden. Auch spezielle Aufgaben der internationalen Mathematik - Olympiade entbehren nicht einer gewissen Schönheit. Besonders ergiebig für die rein geistige Inspirationen ist natürlich das schöne Buch "Sacred Mathematics - Japanese Temple Geometry" der Autoren Fukagawa Hidetoshi und Tony Rothman (Princeton University Press).
In meinem Tagebuch werden so unterschiedliche Themen wie Höhenbestimmung, Viereck in einer Ellipse, Vier Steine und das verlorene Quadrat, Schmetterlingssatz, Feuerbachkreis, Hexagrammum Mysticum, Inversion, Pappos Kreisketten, Satz von Green und Flächenberechnung, IMO-Aufgaben, Foucaultpendel, Rollende Ringe, Steine stapeln, Limiten des Zodiakus, Scheinbare Überlichtgeschwindigkeiten und vieles mehr behandelt.
Das goldene Theorem von Feuerbach
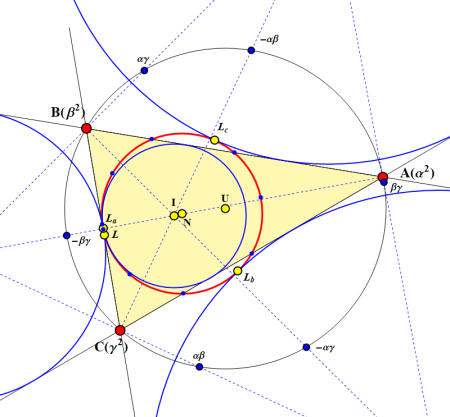
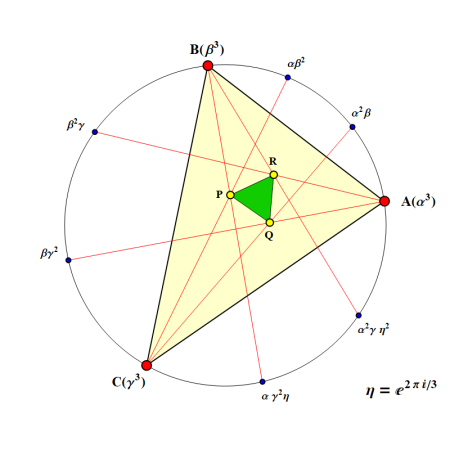
Morley-Dreieck: Eine Perle der Geometrie
Japanische Tempel Geometrie (Sangaku)
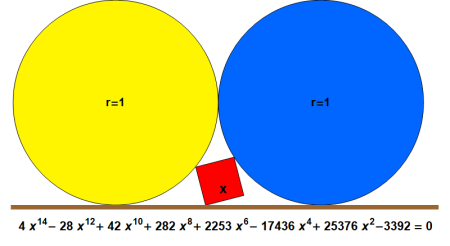
Zwischen den Jahren 1816 und 1821 unternahm in Japan der Mathematiker Yamaguchi Kanzan sechs ausgedehnte Reisen, um sich in seiner Kunst weiter auszubilden. In seinem Tagebuch erwähnte er auch das obige Problem von Morikawa im Tenman Schrein, dessen genaues Entstehungsdatum unbekannt ist. Im einfachsten Fall wird die minimale Seitenlänge eines Quadrates zwischen zwei sich berührenden identischen Kreisen und der Bodenlinie gesucht. Die Tafel zeigte keine Lösung, aber Morikawa schrieb: "Ich wäre sehr glücklich, wenn jemand dieses Problem lösen könnte". Yamaguchi berichtet dann in seinem Tagebuch: "Ich ging mit meinem Freund Takeda in das Haus von Morikawa und fragte ihn nach einer Lösung. Doch er sagte mir, dass er das Problem bis jetzt nicht lösen könne".
Das obige Problem des minimalen Quadrates zwischen zwei Kreisen und einer Grundlinie, welches in dem Buch Sacred Mathematics (Japanese Temple Geometry) von Fukagawa Hidetoshi und Tony Rothmann (Princeton University) als ungelöst dargestellt wird, wurde von mir für die gesuchte Seitenlänge x glücklich auf eine algebraische Gleichung 14ten Grades zurückgeführt. Die relevante Wurzel ist hier x ~ 0.38539836.... Das liegende Quadrat hat die Seitenlänge 2/5 = 0.4, das auf einer Ecke senkrecht stehende Quadrat hat die maximale Länge sqrt{2}-1 ~ 0.4142. Der allgemeine Fall ungleich großer Kreise kann für die Seitenlänge x auf eine Gleichung 20ten Grades zurückgeführt werden. Damit ist dieses sehr schöne und bizarre Sangaku-Problem in unerwarteter Weise gelöst.
Sangaku war in Japan im frühen 19ten Jahrhundert wie ein Glasperlenspiel: Verliebt in eine mathematische Artistik von Aufgaben sehr engem Typus, ohne praktische Anwendung und kein Streben nach einer allgemeinen Theorie.
In der Elementarteilchenphysik gibt es eine empirische algebraische Beziehung zwischen den Massen der drei geladenen Leptonen "Elektron", "Myon" und "Tau". Entdeckt wurde diese Formel 1981 von dem Japaner Yoshio Koide (Koide - Formel). Sie ist in den Massenwerten auf mindestens fünf Dezimalstellen nach dem Komma genau. Anstatt des Massenwertes selber scheint die Quadratwurzel aus der Masse eine fundamentalere physikalische Bedeutung zu haben. Die mathematische Struktur dieser 3-Massen - Formel erinnert außerdem entfernt an den Vier - Kreise - Satz von Descartes.
Ein bis heute ungeklärtes Mysterium zwischen Sangaku und Teilchenphysik...
Aktuelles
kritisch betrachtet
Eine neue Computersimulation im Jahre 2023 des Kosmos (Flamingo project) hat nicht nur Dunkle Materie, sondern auch baryonische Materie und galaktische Winde berücksichtigt. Die Hoffnungen, die S8-Anomalie der Strukturbildung dadurch zu klären, wurden aber enttäuscht. Ursache: anstatt w=-1 (Kosmologische Konstante) doch w = -2/3?
Eine kleine historische Sensation hat sich Ende 2022 in Belgien ereignet: Das verloren geglaubte einzige Videointerview mit George Lemaitre (1894-1966) aus dem Jahre 1964 wurde in einem Archiv wiedergefunden. Es war falsch eingeordnet worden. Nicht nur auf youtube kann man es finden, sondern es existiert inzwischen (Januar 2023) auch eine schriftliche Transkription [arXiv:2301.07198v2] in französischer und englischer Sprache. Ich beabsichtige, dieses legendäre Interview zeitnah ins Deutsche zu übersetzen. Bis jetzt kannte man nur ein schriflich niedergelegtes Interview aus dem Jahre 1938.
Ende 2018 entstand weltweit ein riesiger Medienrummel (Medien-Hype), leider auch unterstützt von der Oxford University, dass das Problem der dunklen Materie und der Dunklen Energie durch die Einführung von zusätzlichen negativen Massen (dark fluid) mit zusätzlicher kontinuierlicher Materie-Erzeugung im Universum sehr einfach gelöst werden könne. Ursache sei einfach ein Vorzeichenfehler, behauptete Jamie Farnes von der Oxford University. (A&A 620, id. A92, 2018) Sofort tauchten aber Gegenstimmen auf, welche die Unmöglichkeit von negativen Massen (träger Masse,schwerer Masse, gravitativer Masse) im Rahmen der Einsteinschen Theorie darlegten. Zudem zeigte sich im Laufe des Jahres 2019 ein schwerer Fehler im Simulations-Programm und die Tatsache, dass sich im Rahmen dieser gewagten These und ihrer korrigierten Simulation die Halos um Galaxien nicht in der beobachten postulierten Form (dunkle Materie) bilden können. Ein öffentlicher Widerruf dieser fehlerhaft falschen Hypothese hat aber nie stattgefunden! Historisch kann man diese Affäre als den NEGATIVE MASS BUG bezeichnen.
Hinweise auf eine angebliche Phase der "Inflation" im frühen Universum zerfallen zu Staub: Im März 2014 veranstaltete ein Team um den Harvard Astronomen J. Kovac (BICEP2) für eine völlig übereilte propagandistische Pressekonferenz (schon einen Tag vorher als Sensation angekündigt!): Man hat in der Hintergrundstrahlung des Universums Signaturen einer Polarisation entdeckt, die angeblich eindeutig auf Gravitations-wellen in einer Inflationsphase des frühen Universums schließen lassen. Der eigentliche Skandal ist, daß man die Daten fast ausschließlich durch MIE-Streuung von Mikrowellen an inter-stellaren Staubteilchen erklären kann und muss - und genau daran hatte das "Team" bei der Auswertung nur sehr unzulänglich gedacht! Ein aggessiver Versuch, die Öffentlichkeit durch Sensation zu täuschen und eine nicht überprüfbare (nicht falsi-fisierbare) Theorie (Inflations - Hypothese) salonfähig zu machen. Der Citation-Index dieser Veröffentlichung ist inzwischen wesentlich höher als ihr Widerruf. Die Raffgier nach Forschungs-geldern und Nobelpreisen treibt auch in der Wissenschafts - Industrie immer bizarrere Blüten...
Nachweis angeblich überall im Universum vorhandener DUNKLER MATERIE in Form von Elementarteilchen gescheitert! Das bis jetzt empfind-lichste Experiment LUX in Sanford/South Dakota USA konnte in einer ersten Phase Ende Oktober 2013 keine WIMPs - Teilchen feststellen, die angeblich einen großen Teil der angeblich existierenden Dunklen Materie ausmachen sollen. Alle früheren angeblichen Nachweise sind somit fehlerhaft gewesen. Ein sehr wichtiges, schönes und befriedigendes Resultat! Die Hypothese der "Dunklen Materie" ist allerdings im Sinne von Ockhams Rasiermesser die wahrscheinlichste "Minimalhypothese", da sie extrem einfach ist und jede dynamische Anomalie durch Hinzufügen exotischer Materie erklären kann. Im Rahmen der Gravitationstheorie (nicht Elementarteilchen - Theorie) wären aber dann "black holes" unterschiedlicher Massen die wahrscheinlichsten Objekte für Dunkelmaterie (Schon Laplace hatte dies 1799 vermutet) Sie wären so etwas wie "die ungeborenen Sterne" des Kosmos, da bei Ihnen die Gasakkretion nicht stattfand oder nicht stattfinden kann. Ob allerdings in der Zukunft der von Teilchenphysikern geschürte "Big Science" Teilchen-Lobbyismus mit der platten Devise - Wir verstehen nichts, können aber alles erklären - das vorherrschende Dogma bleiben wird, wissen nur die Sterne...